![]()
Mean when data set is presented in a frequency table
The following table gives the number of children in each of 20 families. Calculate the mean number of children per family.
Example 2
| Number of children | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Frequency | 4 | 5 | 7 | 4 |
Solution
There are 4 families with 0 children. This gives a total of 0 children.
There are 5 families with 1 child. This give a total of 1 × 5 = 5 children.
Continuing in this way, we have:
It is obviously impossible for a family to have 1.55 children, though this figure can be used by governments and other institutions for planning purposes. In general, the mean or average of a data set is not one of the original values.
Mean when data is presented in a stem-and-leaf plot
Example 3
The stem-and-leaf plot below gives the marks of 12 students in a test.
| 1 | 8 | 9 | ||
| 2 | 2 | 4 | 5 | 6 |
| 3 | 1 | 4 | 9 | |
| 4 | 2 | 3 | 6 | |
| 4\(\mid\)3 means 43 | ||||
Calculate the mean of the marks.
Solution
\begin{align}\text{Mean}\ &=\ \dfrac{18 + 19 + 22 + 24 + 25 + 26 + 31 + 34 + 39 + 42 + 43 + 46}{12}\\\\ &=\ \dfrac{369}{12}\\\\ &=\ 30.75\end{align}Mean when data is presented in a column graph
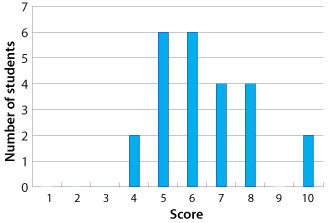
Example 4
The marks obtained for a quiz by a group of students are displayed in the column graph.
Find the mean of the marks.
Solution
\begin{align}\text{Total number of students} &=\ 2 + 6 + 6 + 4 + 4 + 2\\\\ &=\ 24\\\\ \text{Mean} &=\ \dfrac{2 × 4 + 6 × 5 + 6 × 6 + 4 × 7 + 4 × 8 + 2 × 10}{24}\\\\ &=\ \dfrac{154}{24}\\\\ &=\ 6.417\ \text{correct to 3 decimal places}\end{align}